Layout Editor

LAUNCH

• Golaem Shelf:
• Golaem Render Menu: Simulation Cache Layout
• MEL Command: glmOpenCacheLayoutEditor;
• Stand Alone: ./scripts/glm/layout/layoutEditorStandAlone.py

SIMULATION CACHE LAYOUT GUI

The Simulation Cache Layout Editor displays the information about the deformation applied to a Simulation Cache Proxy node.

It is composed of several parts:

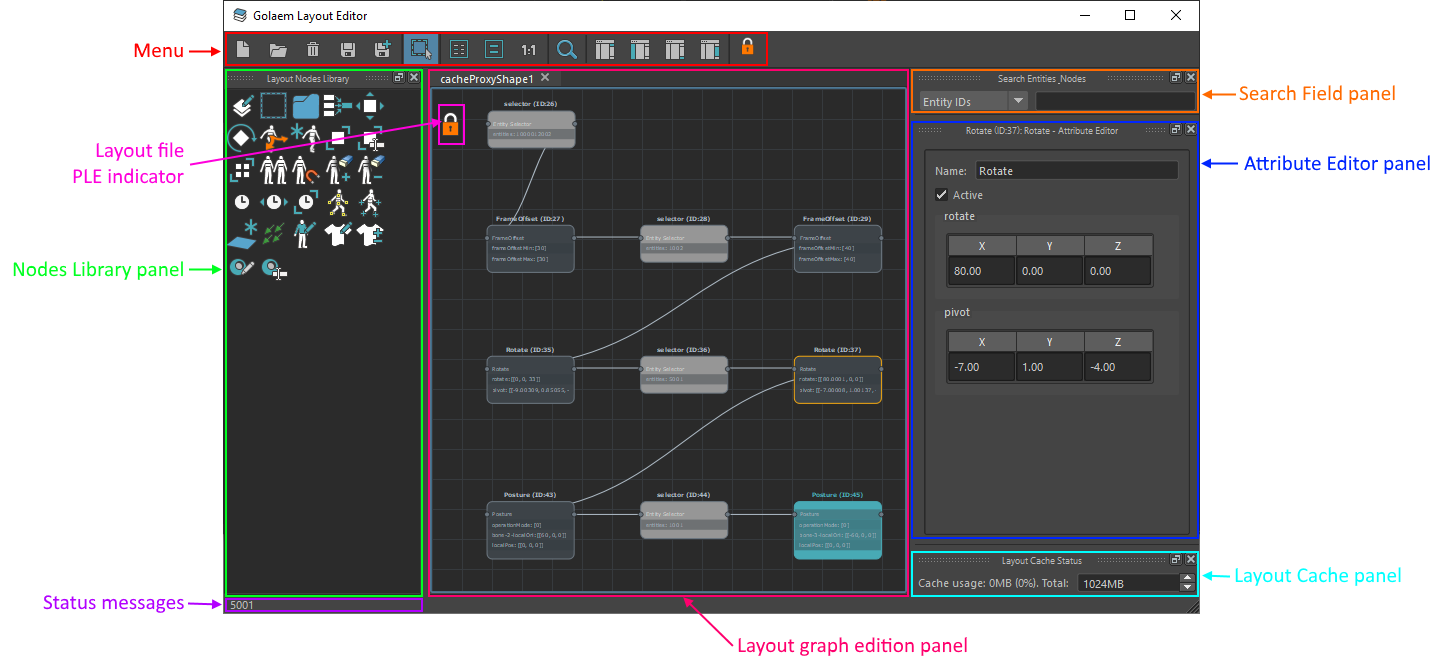
Menu

	Open a new tab in the layout graph edition panel
	Open a layout file in a new tab in the layout graph edition panel
	Save Simulation Cache Layout file (.gscl) with the Deformation Layers added to the Layout Operations Panel for every Crowd Field of every Simulation Cache Proxy in the scene
	Save As Simulation Cache Layout file (.gscl) with the Deformation Layers added to the Layout Operations Panel for every Crowd Field of every Simulation Cache Proxy in the scene
	Clear the current tab in the layout graph edition panel
	Change the settings of the Layout Tool
	Synchronize selection with the DCC toggle button
	Frame the Layout Graph Edition panel view to see all nodes
	Frame the Layout Graph Edition panel view to see the current selection
	Zoom the Layout Graph Edition panel view to the real size
	Open the Simulation Cache Entity Inspector
	Enable/Disable the Search Field panel
	Enable/Disable the Node Library panel
	Enable/Disable the Cache Status panel
	Enable/Disable the Attribute Editor panel
	The PLE indicator indicates that the Layout Editor is currently open with PLE license only. Any file saved from this session will become marked with PLE. This button is not displayed if the Layout Editor found a valid lite license.

Nodes Library panel

This panel display the list of layout nodes that you can use to build your layout graph. Simply drag and drop them from the Layout Node Library to the layout graph edition panel.

	Note node to add a note in the layout graph
	Entity Selector node
	Group node to organize layout in sub graphs
	Merge node to merge layout flows

Transformation Layers

	Translate node to translate character's positions
	Rotate node to rotate character's orientations
	Face to to make characters face toward a given point
	Scale node to scale characters
	Expand node to scale distance between characters

Duplicate Layers

	Duplicate node to duplicate characters
	SnapTo node to duplicate characters and snap them on Population Tool slots
	CreateEntity to create an entity from a character file

Visibility Layers

	Kill node to remove characters from the viewport and the rendering
	Unkill node to restore characters to the viewport and the rendering

Time Edition Layers

	Set Frame to set the frame data to use for characters
	Frame Offset node to offset Simulation Caches for characters
	Frame Warp node to warp Simulation Caches for characters

Posture Edition Layers

	Posture node to edit the orientation of Character Bones
	Rig node to import the Simulation Cache as a keyframed Maya skeleton and allow to edit curves
	Look At to make characters look at a given point
	BlindData to edit the blind data values (like blend shapes)
	Ground Adaptation node to edit the ground adaptation mode
	PlayAnimation to replay an animation file on an entity

Trajectory Edition Layers

	Trajectory Vector Field node to constrain the trajectory of Characters to a Vector Field
	Edit Trajectory node to edit the trajectory of characters

Geometry Edition Layers

	Set Rendering Type node to edit the Rendering Type assigned to a Character
	Set Mesh Assets node to edit the Mesh Asset assignment of a Character
	Add/Remove Mesh Assets node to edit the Mesh Asset assignment of a Character
	Replace Shader node to edit the Shader assigned to a Character Mesh Asset
	Set Shader Attribute node to edit the Shader Attribute value assigned to a Character Shader
	Set Attribute node to edit cache attribute values, that can be used in previz or rendering operations
	Mirror Geometry node to mirror the geometry of a Character
	Replace LOD Distances node to replace the lod distance of a Character file

Layout graph edition panel

The layout graph edition panel is the place where you can edit the layout graph. Each tab represents a different layout graph. The tab can can be renamed by right clicking on the current tab:

Rename the current tab by right clicking on it

Understanding the graph

You can zoom in/out in the graph by using the mouse scroll.

You can pan in the graph by holding the Alt + mouse middle click while moving the mouse in the Layout Graph Edition panel.

Nodes

There are two kind of nodes:

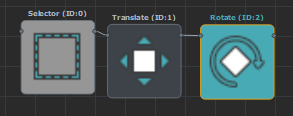
• 'selector' nodes changes the current selection of entities in the flow. They are represented in light gray:
  
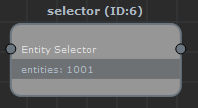
• 'operator' nodes perform operations on the currently selected entities in the flow. They are represented in dark gray:
  

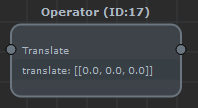
Some nodes are both a selector and an operator: they perform an operation on the currently selected entities in the flow, but also changes the current selection of entities in the flow. This is for instance the case for the duplicate and snapTo nodes: they duplicate the currently selected entities while changing the selection to be the duplicates entities from now on.

Execution flow

The layout graph executes any node that contributes (is directly or indirectly connected on the left) to the root node (colored in cyan).

A node that is connected to the left of another node will always be executed first.

When a merge occurs, all nodes connected to the left of the merge node will be executed first, but there is no guaranty about the order in which it's going to be executed. If the order of execution matters, then nodes should be connected in the same single line of execution.

For instance, a layout graph that looks like this:

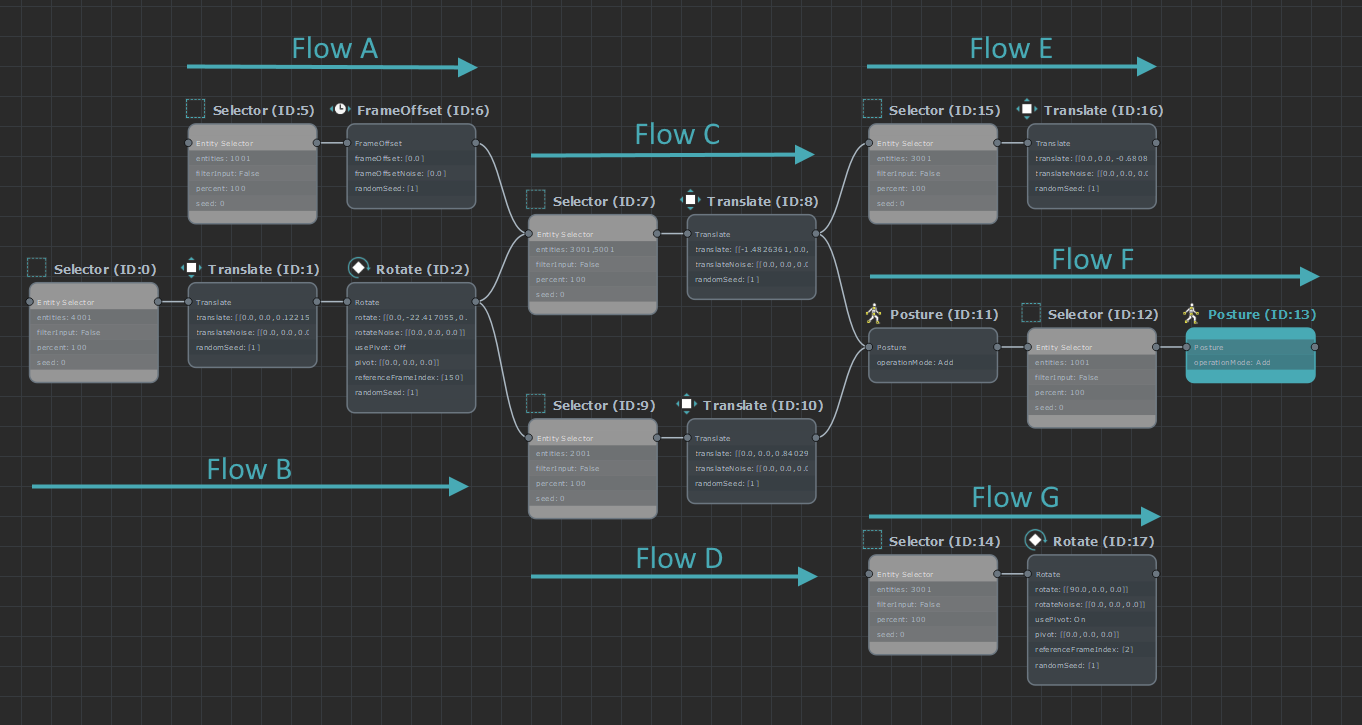
Will have the following execution flow:

• Flow A will be executed before flow C, but may be executed after D as it is not connected to its left
• Flow B will be executed before both flow C and flow D
• Flow C and D will both be executed before Flow F
• The Operator that is at the beginning of Flow F will use a selection that is a union of the selections from Flow C and D
• Flow F is executed last (as it includes the root node)
• Flow E will never be executed (it's not connected to the left of the Root node)
• Flow G will never be executed (it's not connected to the left of the Root node)

Automatic replacement of duplicate Ids with node output syntax

From Golaem 7.1 and higher, it is possible to stack several layouts on a cache. That implied a change in the duplicate entities ID management. As the duplicate IDs are a general pool, shared by the whole layouts stack, generating a new duplicate ID in a low index layout file, would shift all duplicate IDs of the higher indices ones. If the IDs are stored as they are generated, this could lead to a second layout file editing different entities onces the first one grow with more entities. To avoid that, the duplicate IDs of a layout are now automatically replaced by a syntax indicating that their are the output of a duplicate/snapTo node. This syntax is o([nodeId], [entityIndex]), standing for "output of node" nodeID, [entityIndex]th entity in node output. With that modification, all tweaks added to an entity duplicated in the same layout will stay consistent.

Editing the graph

Adding a node

• Drag and drop a node from the Layout Nodes Library
• Hit the 'tab' key in the Layout Graph Edition Panel, which will open a menu in the view:
  
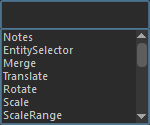
  Type the node type name or simply select the node to add from the list to add it to the graph.
• Use Maya translate / rotate / scale manipulators, while some entities are selected (in F9 mode). It will add a selection + node to the end of the root node with the current selection
• Double-click on a layout editor node in the shelf : if the selection is valid, it will add a selection + node to the end of the root node, else it will stack the node after the root node (if it exists). Double-clicking a selector node creates a selector with the current selection.

Removing a node

Select the node in the Layout Graph Edition Panel and hit the 'delete' key

Moving a node

• drag and drop the node in the Layout Node Library
• select the nodes to automatically layout and hit the 'L' key

Editing a node

• click on a node to show/edit the list of its parameters in the Attribute Editor panel

Check the meaning of each parameter directly in the node's documentation page

Connect/Disconnect nodes

To connect a node, you can:

• left click from one node plug to the other node's plug
• middle click from anywhere on the node to anywhere on the other node to connect
• move the node over an existing connection to insert the node between the two other connected nodes

To disconnect a node, you can;

• select a connection and hit the 'delete' key
• move the node to disconnect while holding the 'ALT' key
• use the cut tool by holding the 'ALT' key, while cutting the connection(s)

Set root node

Select a node and hit V key, or right click on the node and select the 'Set as root' option

Grouping / Ungrouping nodes

Nodes can be grouped by selecting some nodes, then right clicking and clicking 'Group'. They can also be dragged and dropped on an existing group node, or copied from somewhere and paste in the group. Ctrl + G key also groups current selection under a new node.

Nodes can be ungrouped by selecting a group node, right clicking and clicking 'Ungroup'.

Navigation one step "up" from current group  can be achieved with a Ctrl + double clic.

Misc

A node can be enabled or disabled by right clicking on it and selecting the 'Enable' or 'Disable' option.

Nodes can be copied/pasted:

• by using the Ctrl-C (to copy) and Ctrl-V (to paste) key shortcut
• by using the Ctrl-D (to duplicate) key shortcut
• by right clicking on the node(s) to copy and selecting the 'Copy' option, and then right clicking in the same Layout Graph Edition panel and selecting the 'paste' option

This panel displays the amount of RAM that is currently used by the Golaem Cache. Whenever the cache is full, old frames in cache will be dropped to add new frames.

Status Messages

This line will display the currently selected entities in Maya.

Layout Editor Display Level of details

The editor can use three different display modes, depending on the zoom level, to keep if fast and readable.

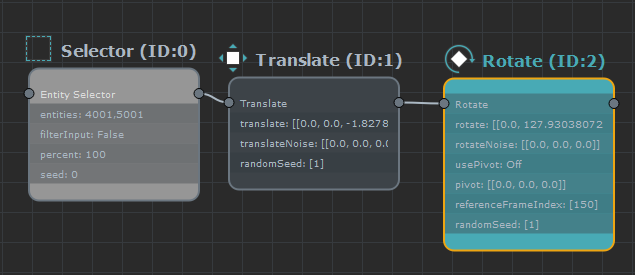
While the editor is focused on a few nodes, the level of detail is maximum, showing each node parameter and its value.

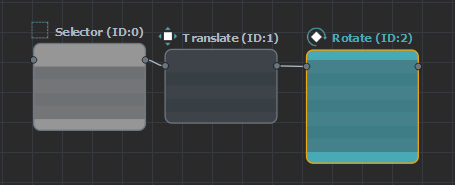
When the editor is being zoomed out, the parameters are not displayed anymore to (performance saving) as they are not readable anymore.

When zoomed out further, the title logo starts to be unreadable, and is moved in a bigger version, displayed inside of the node, which helps to keep track of what are the transformation types of each node.